At social gatherings I often find myself alone after I answer the “what do you do?” question. “What I did” was complex, but I tried to simplify it by saying that I was a statistician. I knew what would ensue, the questioner’s dazed eyes would quickly dart toward the exits, or stealthily search for a lively conversation or discover a “friend” to save him. Someone really desperate might pour a drink on his shoes and excuse himself to get another drink. Over the years, I became very familiar with the “caged animal” look.
But statistics are really fun, they really are. Probability and statistics are part of our everyday lives. What is the probability of rain or snow? What is the probability that we will see a bald eagle? What is the likelihood that a relative will call? Statistics can help us answer these questions.
And we only need to rely on a few basic rules in probability to solve even the most complex question. (Okay, I might be exaggerating here.) What makes statistics seem complicated is that we use our own language to communicate with the world. In its purest form, mathematics has been called the poetry of the universe because it is universal, it can reveal the language of nature, and predict an unpredictable world.
The birthday paradox is a beautiful example of prediction. How many times have you been at a party and found someone with the same birthday? You might think the odds of this occurring to be 1 in 365 or 1/365 or <1%, in fact, in a room of 50 people, there is almost a 97% chance that there will be two people who share a birthday (not necessarily yours). In a room with as few as 23 people, there is a 50% chance that there will be two people with the same birthday. In a party of 75 people there is greater than a 99% chance.
Inconceivable, right? But it is true, it is called the Birthday Paradox and you can confirm it at your next event.
You need to know only a few probability concepts to calculate this yourself.
The first concept is that the probability of sequential events is the single event probability to the nth power where “n”= the number of events. Huh? Let me explain in English. If you flip a fair coin (with a 50/50 chance of heads) and get heads three times, the probability of getting this sequence is ½*½*½ (or .53) which is 12.5%. Conversely the probability of not getting this sequence is 100%-12.5%= 87.5%. Pretty simple, right? Let’s use an example where there are more than 2 outcomes (heads or tails), a simple die, where a single roll can result in a 1,2,3,4,5, or 6. Let’s calculate the probability of getting a “2” three times in a row. The probability of getting a “2” when you roll a die once is 1/6 (because there are 6 possible outcomes, right?). To get a “2” three times in a row would be 1/6 * 1/6 * 1/6 (or .1673)=0.46% chance. So the chance of NOT rolling a “2” three times in a row is (100%-.046%)=99.54%…you should take that bet.
Okay, we are almost there. Statisticians frame the solution to the birthday paradox by calculating the probability there will NOT be two people sharing the same birthday at the event and subtracting 100% from that (just like we did when we calculated an 87.5% chance of not rolling heads three times in a row, or a 99% chance of not rolling a “2” 3 times in a row). So it is 100% MINUS (the probability of not finding people with the same birthday).
The next part is a little tricky because we need to calculate the number of different pairs in a group of 50 (this will be your “event” like flipping a coin). To calculate the number of possible pairs, we use a formula (which is a little complicated since it involves factorials) to save us the trouble of manually listing all of the possible pairs. To simplify the formula, if there were 50 people at the party, the number of pairs would be (50*49)/2, or 1225 (if there were 30 people, the formula would be (30*29)/2, etc.).
So 1225 is the number of events because it is the number of possible pairs.
Next, we need to know the probability of 2 people not having the same birthday. Let’s frame it more simply, what is the probability of meeting a random person off the street with your birthday? 1/365 or .0028, right? So the probability of two random people not having the same birthday is1- (1/365) = 364/365 (which is .997). (I am ignoring both twins and February 29th birthdays because it makes it too complicated.)
Now we just put the pieces together. To find the probability of two people having the same birthday. when there is a roomful of 50 people, we are going to find the probability of 2 people not sharing a birthday and subtract it from 1.
To plug in our numbers: we multiply the probability of two random people not sharing a birthday (364/365=.997) and then we multiply that probability each time for the number of possible pairs (or events like a roll of a die). We know that there are 1225 pairs in a room of 50 people. We know that the probability of a single event of two people NOT sharing the same birthday is 364/365=.997. So the calculation would be
1-.9971225 =97% (rounded up).
Therefore in a party of 50 people there is a 97% chance that at least 2 people share the same birthday.
Congratulations, you have just solved a problem found in advanced statistics class! Now maybe I can find someone to talk to me at parties.
Angela Rieck was born and raised on a farm in Caroline County. After receiving her PhD in Mathematical Psychology from the University of Maryland, she worked as a scientist at Bell Laboratories in New Jersey. Throughout her career, she held management jobs at AT&T, HP and Medco, finally retiring as a corporate executive for a large financial services company. Angela is also a wife, mother and an active volunteer serving on the Morris County School Board for 13 years and fostering and rehabilitating over 200 dogs. After the death of her husband, Dr. Rieck returned to the Eastern Shore to be with her siblings. With a daughter living and working in New York City, she and her dogs now split their time between the Mid-Shore and Key West, FL.
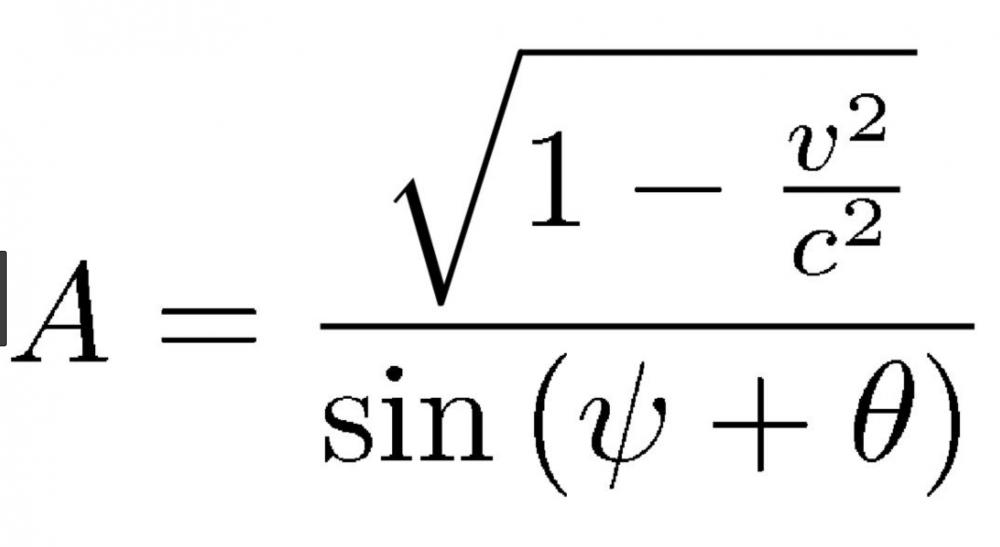


Angela Rieck says
Sorry, there are some problems with the text because superscripts (exponents) are not showing clearly. The probability of getting heads 3 times in a row is 5 to the 3 power or .5x.5x.5= 12.5%. The probability of getting a “2” 3 times in a row on a die is .167 to the third power (or .167 X.167 X.167). The probability of have two birthdays in a room of 50 is:
1-(.997) to the 1225 power or (.997 x .997 X .997… for 1225 times). Sorry about that, I guess statistics is not a universal language after all.